Research Overview
Our current research aims to theoretically model, understand, and predict a variety of nonequilibrium phenomena in complex material systems and reveal the underlying intrinsic mechanisms. The focus is on micro- and nano-structural properties and dynamical behaviors in solid and soft materials and active matter, particularly the formation and dynamics of complex patterns and intricate microstructures involving effects of elasticity, plasticity, and topological defects, as well as nonlinear, nonrelaxational dynamics in active and living systems. Example systems include, but not limited to:
• Novel 2D materials and heterostructures, with focus on structures and dynamics of topological defects (e.g., dislocations and grain boundaries), grain growth and evolution, ordering, moiré patterns, and mechanical properties.
• Spatiotemporal systems that are out of equilibrium, particularly nonpotential, nonrelaxational dynamics in active chiral patterns or crystals consisting of self-propelled and/or self-spinning particles, and complex fluid convection patterns with the emergence of spiral defect chaos.
• Strained solid films, such as epitaxial nanostructures with morphological and compositional modulations and/or topological defects.
Most of our efforts are based on the development of efficient multiple-scale methods for modeling the above nonequilibrium systems. It involves approaches and analyses at different levels/scales of description that incorporate continuum density-field theory and microscopic details of crystalline/periodic structures, defect configurations, or nanophases. Examples include the phase field crystal (PFC) method, “slow”-scale amplitude equation formalism, mesoscopic-level coarse-grained modeling, and hydrodynamic coupling.
Development of the multiscale PFC method
The phase field crystal (PFC) method is a predictive density-field approach bridging microscopic and mesoscopic scales and incorporating elasticity and plasticity. It can resolve microscopic crystalline details or individual defect structures, maintaining atomic-level spatial resolution through a continuum density-field description, and model dynamical processes at diffusive timescales. The length scale restriction at microscale can be further mitigated via the corresponding mesoscopic complex amplitude formulation (as illustrated in the above figure), which enables us to examine large-scale intricate patterns and interfacial profiles (e.g., for 2D materials with system size up to tens of microns).
We have been working on the development of PFC and amplitude models for a variety of material systems (including both passive solid/soft materials and active matter), to identify and predict complex structural and elastoplastic properties and dynamical mechanisms that are inaccessible to conventional techniques. Our research has been combined with atomistic or particle-based methods (such as density functional theory (DFT) and molecular dynamics (MD)) and continuum theories, through collaborations with experts across multiple disciplines.
Study of 2D graphene-type materials and heterostructures
Two-dimensional (2D) material systems, such as graphene, hexagonal boron nitride (hBN), silicon carbide (SiC), transition metal dichalcogenides (TMDs), and chromium trihalides, are of tremendous research interest due to their extraordinary electronic, mechanical, thermal, and magnetic properties as a result of dimensional confinement. Based on the development of multiscale PFC models, we have been working on the structural and dynamical properties of these 2D materials, particularly those related to material elasticity, plasticity, topological defects (dislocations and grain boundaries), heterostructures and moiré patterns.
Some sample PFC modeling results are shown in the above figure, including (a) grain boundary energy of monolayer hBN across the whole range of misorientation angle (for both symmetrically and asymmetrically tilted boundaries; see Phys. Rev. Lett. 118, 255501 (2017)), (b) dislocation core transformation during the grain boundary motion and grain rotation of hBN (Acta Mater. 225, 117583 (2022)), and (c) an example of moiré pattern in a graphene/hBN bilayer with 0.66º twist angle (see Phys. Rev. Mater. 7, 024003 (2023)). Our goal here is to understand, predict, and control the formation and dynamics of complex microstructures or patterns in both monolayer and multilayer 2D material systems, especially those emerging in large scale samples synthesized via epitaxial growth with realistic, long relaxation times.
Study of complex dynamics in chiral active matter
One of our current research efforts is put on the field-theoretical study of active matter, in particular the nonequilibrium active pattern formation, crystallization, and the corresponding defect and grain dynamics in active and living systems. These complex systems are composed of self-propelled and/or self-spinning artificial or biological components (i.e., self-driving “active particles”) operating with self-sustaining energetic sources or propulsive forces. Compared to passive solid or soft materials, such active systems not only naturally involve multiple spatial and temporal scales, but also possess a key feature of being intrinsically out of equilibrium. This leads to a vast variety of complex dynamical behaviors and collective phenomena, as being actively studied in the current experimental, theoretical and computational research.
Our main interest here is to develop and apply the multiscale density-field approach to tackle the vast complexity of these nonequilibrium, nonpotential systems, exploring and predicting the emergence of collective dynamical states. This includes active crystalline behaviors, pattern-forming processes, and dynamical properties of active topological defects. Some of our recent modeling results and predictions are shown in the figure here, including (a) the dynamically frustrated state of active crystallite as a result of competition between self-propulsion and self-spinning of chiral particles (Phys. Rev. Lett. 125, 218002 (2020)), (b) persistent dynamics of topological defects in active smectics with boundary confinement (Commun. Phys. 5, 294 (2022)), (c) the formation of active chiral patterns breaking 2D parity-time symmetry, as caused by effects of nonreciprocal forces which break Newton’s third law among single species (arXiv:2404.10093), and (d) self-fission and fragmentation of self-rotating grains in chiral crystals with odd elasticity (Proc. Natl. Acad. Sci. U.S.A. 122, e2511350122 (2025); see also the related Highlight).
Nanostructure dynamics and defects in strained films
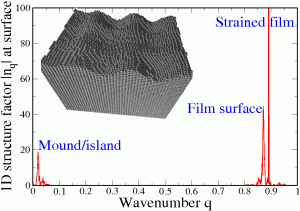Strained film heteroepitaxy, including a wide variety of epitaxial growth techniques such as MBE, CVD, VPE, LPE, etc., has become one of the most important methods in the manufacturing and processing of material nanostructures (including strained islands or quantum dots, nanowires, etc.). Our focus is put on understanding the key effects on the control and organization of such nanostructures in both single-component and alloy films (see an example shown on left, as in Phys. Rev. Lett. 101, 158701 (2008)). This involves the stress-induced effects and microstructures either on the film surface or across the interface, the coupling between morphological profiles and compositional inhomogeneity, interfacial diffusion vs surface mass transport, and the dependence on various growth parameters (e.g., temperature and growth rate).
We are also interested in the defect dynamics and structural vs compositional evolution in strained solid films, which are among the main factors that strongly influence material properties, functionality, and potential device applications. Our research is focused on the coupling and interaction among topological defects (particularly grain boundaries and dislocations), phase separation in alloy films (with an example shown on right), and film surfaces or interfaces. We also examine the interplay between the slowly varying profiles of interface, defects, or composition and the underlying microscopic crystalline structure, which leads to important effects of lattice pinning with significant impacts on interfacial evolution and structural dynamics (see e.g., Phys. Rev. E 87, 012401 (2013) and Phys. Rev. E 93, 022803 (2016)).
Complex pattern formation and defect dynamics
The spontaneous formation of complex modulated structures or spatiotemporal patterns is ubiquitous in both natural and synthetic material systems. Among the least understood are spatially extended systems driven far from equilibrium, for which the governing dynamics is nonrelaxational. One of our interests is in addressing the fundamental mechanisms underlying the complex phenomena of ordered vs chaotic pattern evolution in such nonequilibrium, nonpotential systems, such as the prototypical system of Rayleigh-Bénard convection. Stability, motion, and interaction of individual defects are found to play a key role in the transition to the state of spiral defect chaos, and also in the possible persistent dynamics of the pattern (see Phys. Rev. E 84, 046215 (2011) and Phys. Rev. Fluids 5, 093501 (2020)).
