My Research

My main research interest is a long-term project to make fundamental computations in motivic homotopy theory. This research is supported by a grant from the National Science Foundation.  This page summarizes my research work for non-experts.  If you would like more detail, see my pages on motivic homotopy theory and other research interests.

Here is a quick introduction to the topic of my research, intended for undergraduate-educated scientists:

The geometric objects of interest in algebraic topology can be constructed by fitting together spheres of varying dimensions. The homotopy groups of spheres describe the ways in which spheres can be attached to each other. From the viewpoint of algebraic topology, detailed knowledge of these groups would lead to a classification of geometric objects. We summarize the state of previous knowledge of the stable homotopy groups of spheres through dimension 61 and provide information in dimensions 62 through 90. It is a highly counterintuitive fact that some high-dimensional spheres can be viewed in more than one way from the perspective of differentiability. We enumerate these differentiable structures through dimension 90, except for dimension 4.

This excerpt comes from the article
D. C. Isaksen, G. Wang, and Z. Xu, Stable homotopy groups of Spheres, Proceedings of the National Academy Sciences, 2020.

Here is a 10-minute video research statement in which I explain the overall ideas in my research program.  If you’d like to see additional details, here are a few recorded presentations:

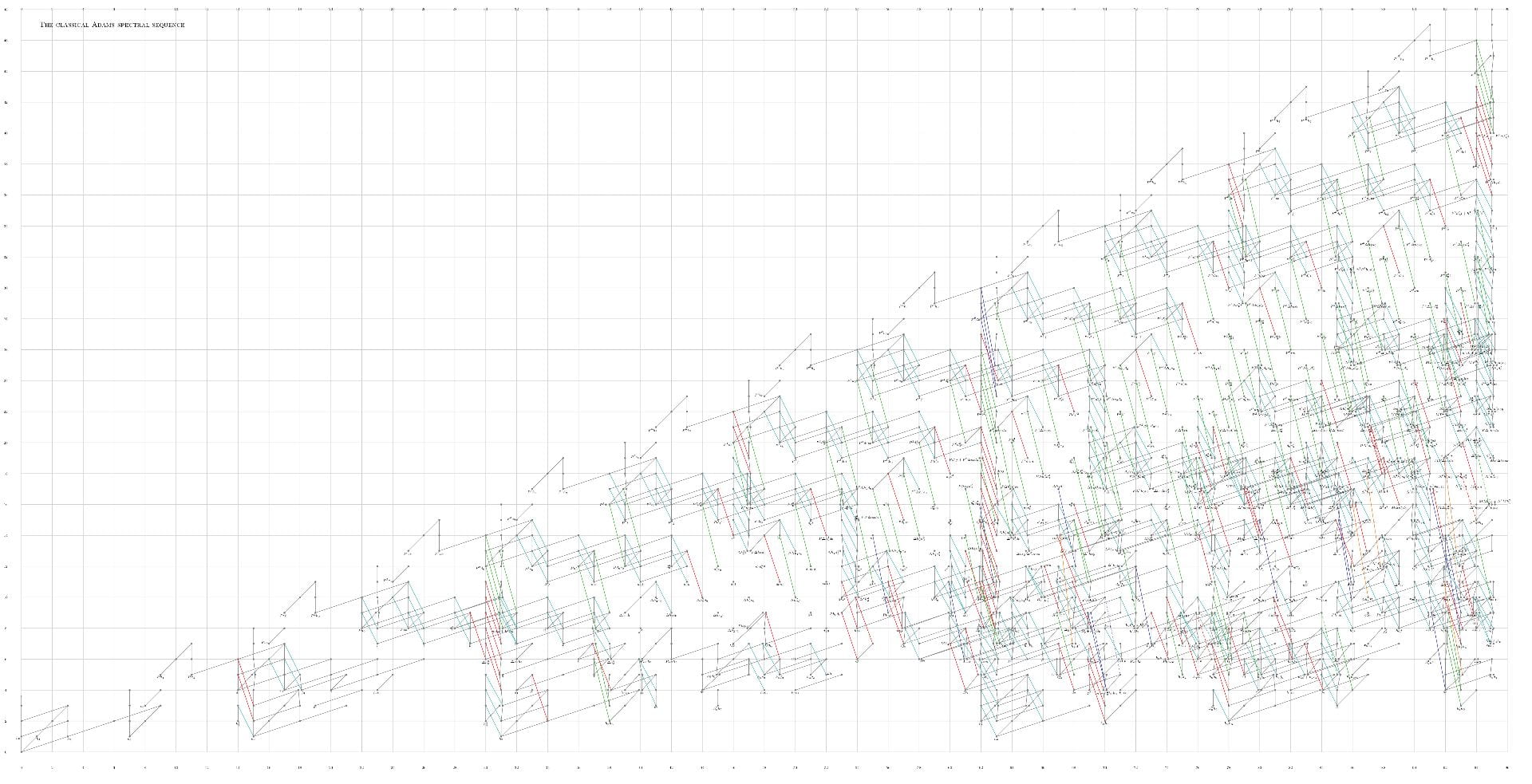
The chart below represents one possible approach to the problem of computing stable homotopy groups.  Each dot represents a particular combination of spheres.  The lines indicate certain relationships between these different combinations.

I use a tool called the Adams spectral sequence to carry out these computations.  It is delicate, intricate, subtle, and complicated, but it is also understandable with enough insight and patience.  Each time we understand a new part of the machinery, another layer of complexities becomes accessible for further study.  By grappling with the difficulties of the Adams spectral sequence, we are widening human knowledge and developing new skills for thinking about abstract mathematics.

Much of my work is supported by large machine computations.  In essence, the machine computations are specific linear algebra problems in very high dimensions.  The image below shows the reduced echelon form of a particular matrix of size 10127 x 11267.  For experts, it is the differential in a minimal resolution of the field F2 over the Steenrod algebra, in homological degree 6 and internal degree 100, with respect to a certain ordering on the Milnor basis.  Click the image to see a larger version.  I recommend that you zoom in until you can see the individual pixels.  This picture was generated by Joey Beauvais-Feisthauer, using data obtained from the SpectralSequences project.

Sometimes people (including mathematicians) ask how we are confident that our complicated, lengthy, and detailed computations are correct.  This is an excellent question that deserves careful consideration.  First of all, we rely on computer calculations whenever possible.  However, eventually we want to go beyond what can be verified by computer.

The different parts of the structure that we are calculating are linked in multiple complicated ways with each other.  As a result, when we make a mistake, inconsistencies typically arise quickly with other parts of the calculation.  This keeps us on the right track because the method itself catches many errors.

One possible analogy is to building a model of a ship.  Imagine having all of the parts of a kit for building a ship, but no instructions.  With enough patience and attention to detail, you might be able to figure out how to build the ship.  You might make mistakes along the way, which you can correct later when you realize that other parts won’t fit.  In the end, if you’ve used all the parts, and the result floats in water, then you’ve probably built the model correctly.